ニュートンの補間公式

ニュートンの補間公式

　いくつかの点での関数値を与えて，そのような値を持つ関数の別な点での値を推測しようとすることがあります。このようなことを補間と言います。例えば，

ｘ＝０で，ｙ＝４であり，ｘ＝２で，ｙ＝８

であったとします。このとき，

ｘ＝１のとき，ｙはいくつか

と言う問題です。勿論実際には，この前提だけでｙの値は決定できません。しかし，座標平面上の点（０，４）と（２，８）を直線で結んでその中点から（１，６）と推測するのは自然です。

　これは，この関数を１次関数と見て，ｙ＝２ｘ＋４と推測したことになります。

　この方法は多項式補間と言われるものの最も簡単な場合で，求める関数を最も次数の低い多項式で与えられる関数と考えたものです。

多項式補間

　多項式補間は次の事実に基づいています。

ｘ_０＜ｘ_１＜ｘ_２＜・・・＜ｘ_ｄ－１＜ｘ_ｄを相異なるｄ＋１個の数とし，
ｙ_０，ｙ_１，・・・，ｙ_ｄ－１，ｙ_ｄ，をｄ＋１個の数とする。このとき，

ｙ_ｉ＝ｆ（ｘ_ｉ），　ｉ＝０，１，・・・，ｄ

となる高々ｄ次の多項式ｆ（ｘ）が唯一つ存在する。

　この定理は高校の数Ⅰの範囲での定理ですが，確認の意味で簡単に証明をしましょう。

一意性（存在したとすると唯１つであること）

　ｆ（ｘ），ｇ（ｘ）がそれぞれ上の条件を満たす高々d次の多項式とします。このとき，F(x)=ｆ(x) - ｇ(x) と置くと，Ｆ（x）は高々ｄ次の多項式で，方程式Ｆ（x）=0はｄ＋１個の解ｘ_ｉ（ｉ＝０，・・・，ｄ）を持ちます。

　一方，０でない高々ｄ次の多項式は高々ｄ個の解しか持ちません。従って，Ｆ（ｘ）は零多項式でなくてはなりません。故に，ｆ（ｘ）＝ｇ（ｘ）となります。

　存在

実際にこのような多項式が存在することは，具体的にそのような多項式を作ることで示します。この作り方は色々ありますが，ここではニュートンの補間公式と言われるものを紹介します。

ニュートンの補間公式

ｆ_ｊ（ｘ）を，ｆ_ｊ（ｘ_ｉ）＝ｙ_ｉ，ｉ＝０，・・・，ｊ　を満たす高々ｊ次の多項式とすると，ｆ_ｊ＋１（ｘ_ｉ）＝ｙ_ｉ，ｉ＝０，・・・，ｊ，ｊ＋１　を満たす高々ｊ＋１次の多項式ｆ_ｊ＋１（ｘ_ｉ）は適当な定数ｃ_ｊ＋１に対して次の式で与えられる。

ｆ_ｊ＋１（ｘ）＝ｆ_ｊ（ｘ）＋ｃ_ｊ＋１（ｘ－ｘ_０）（ｘ－ｘ_１）・・・（ｘ－ｘ_ｊ）

　上のようにして決めた，ｆ_ｊ＋１（ｘ）がｆ_ｊ＋１（ｘ_ｉ）＝ｙ_ｉ，ｉ＝０，・・・，ｊを満たすことは，上式の右辺第２項がｘ＝ｘ_ｉ，ｉ＝０，・・・，ｊで０になることから直ちに分かります。またｆ_ｊ＋１（ｘ_ｊ＋１）＝ｙ_ｊ＋１となることは，これを満たすようにｃ_ｊ＋１を決めることで得られます。

　それには，上の式の右辺で，（ｘ＝ｘ_ｊ＋１を代入した式＝ｙ_ｊ＋１）の方程式を解いてｃ_ｊ＋１を決めれば求めるものが得られます。。

　上の操作を，定数多項式ｆ_０（ｘ）＝ｙ_０から始めて，ｊ＝ｄまで行えば求めるものが得られます。

例

　ｘ_０＝－２，ｘ_１＝０，ｘ_２＝２，ｘ_３＝５，ｙ_０＝－１，ｙ_１＝５，ｙ_２＝３，ｙ_３＝２０

とします。

ｆ_０（ｘ）＝ｙ_０＝－１，

ｆ_１（ｘ）＝ｆ_０（ｘ）＋ｃ_１（ｘ－ｘ_０）
　　　　＝－１＋ｃ_１（ｘ＋２）＝－１＋３（ｘ＋２），

　　（ここで，-１＋ｃ_１（ｘ_１＋２）＝ｙ１より，ｃ_１＝３を求める。）

ｆ_２（ｘ）＝ｆ_１（ｘ）＋ｃ_２（ｘ－ｘ_０）（ｘ－ｘ_１）
　　　　＝－１＋３（ｘ＋２）＋ｃ_２（ｘ＋２）ｘ＝－１＋３（ｘ＋２） - （ｘ＋２）ｘ，

　　（ここで，-１＋３（２＋２）＋ｃ_２（２＋２）２＝３より，ｃ_２＝－１を求める。）

ｆ_３（ｘ）＝ｆ_２（ｘ）＋ｃ_３（ｘ－ｘ_０）（ｘ－ｘ_１）（ｘ－ｘ_２）
　　　　＝－１＋３（ｘ＋２） - （ｘ＋２）ｘ＋ｃ_３（ｘ＋２）ｘ（ｘ－２）
　　　　＝－１＋３（ｘ＋２） - （ｘ＋２）ｘ＋（ｘ＋２）ｘ（ｘ－２）/３
　　（ここで，-１＋３（５＋２）-（５＋２）５＋ｃ_３（５＋２）５（５－２）＝３より，ｃ_３＝１/３を求める。）

と求める式が得られます。

c_iの計算（差分法）

ニュートンの補間公式は求める多項式を

ｆ（ｘ）＝ｃ_０＋ｃ_１（ｘ－ｘ_０）＋ｃ_２（ｘ－ｘ_０）（ｘ－ｘ_１）＋・・・
　　　　　＋ｃ_ｄ（ｘ－ｘ_０）（ｘ－ｘ_１）・・・（ｘ－ｘ_ｄ－１）

として，順次ｃ_０，ｃ_１，・・・ｃ_ｄを求めていく方法です。筆算でこれらを求める場合は上のような方法で良いのですが，プログラムとして表す場合はもう少し体系的な取り扱いが必要です。上の方法を精密化してプログラムとして書けるようにしましょう。

まず，ｃ_０＝ｙ_０は直ちに得られます。

１．ｃ_１の計算：上式にｘ＝ｘ_１を代入することで，

ｃ_１＝（ｙ_１-ｙ_０）/（ｘ_１-ｘ_０）

が得られます。

２．ｃ_２の計算：上式にｘ＝ｘ_２を代入することで，

ｃ_２＝｛［（ｙ_２-ｙ_０）/（ｘ_２-ｘ_０）］-［（ｙ_１-ｙ_０）/（ｘ_１-ｘ_０）］｝/（ｘ_２-ｘ_１）

が得られます。この式はｃ_１に比べて複雑ですが，

ｙ’_１＝［（ｙ_２-ｙ_０）/（ｘ_２-ｘ_０）］，ｙ’_０＝［（ｙ_１-ｙ_０）/（ｘ_１-ｘ_０）］

と置くと，

ｃ_２＝（ｙ’_１-ｙ’_０）/（ｘ_２-ｘ_０）

となり，ｃ_１と良く似た形になります。

　このような形の式を差分と言います。ｃ_１は一階の差分，ｃ_２は差分の差分ということで２階の差分と言います。

　ｃ_ｉを求めるために差分の定義をしましょう。

差分の定義

ｆ［ｘ_ｉ］＝ｆ（ｘ_ｉ）　と０階の差分を定め，以下帰納的に

ｆ［ｘ_ｉ，ｘ_ｉ＋１，・・・，ｘ_ｉ＋ｊ］＝｛ｆ［ｘ_ｉ＋１，ｘ_ｉ＋２，・・・，ｘ_ｉ＋ｊ］-ｆ［ｘ_ｉ，ｘ_ｉ＋１，・・・，ｘ_{ｉ＋ｊ－１}］｝/（ｘ_ｉ＋ｊ-ｘ_ｉ）

によって，ｊ階の差分を定めます。

　この定義に従えば，上の式から，

ｃ_１＝ｆ［ｘ_０，ｘ_１］

ｃ_２＝ｆ［ｘ_０，ｘ_１，ｘ_２］

となることが分かります。そして一般に，

ｉ＝０，１，２，・・・，ｄに対して

ｃ_ｉ＝ｆ［ｘ_０，ｘ_１，・・・，ｘ_ｉ］

が成立します。この事実を使ってプログラムを書きましょう。

プログラムの概要

　プログラムの概要を考えましょう。ニュートンの補間公式で得られる関数のグラフを表示することにします。

　多項式の次数ｄとd+1個の数とそれに対応する関数値をプログラムの中に書くことにします。このとき，

与えた点をグラフに表示し
ニュートン補間した関数のグラフをその上に描く

　さて，以上の処理を実現するプログラムを書いて見ましょう。

ニュートンの補間公式による関数を求める以外は全く標準的です。

基本データの入力部分

　入力に必要なデータが比較的あるので，Input 文による入力ではなく，プログラムに書き込むことにします。データファイルを別に用意し，それから読み込むようにすることも可能ですが，ここでは簡単のため，プログラムに書き込んで使うことにします。

必要なデータは求める多項式の次数と，点と値との対応データです。

Public PDEG
PDEG = 7 :'多項式の次数
'----------------------
'データの個数＝PDEG+1
'     x   y  
Data -8,  2
Data -5,  3
Data -3,  1
Data  0,  2
Data  2,  1
Data  5,  3
Data  8, -4
Data  9, 1
'----------------------

のようにすることにします。PDEG はPolynomial Degree のつもりです。上の場合，高々７次の多項式で補間すると指定してします。対応データは　Data 文で書きます。対応データの個数は次数＋１ですから，今の場合，８個のデータが必要です。 y のデータは同じでも構いませんが，ｘの値は全て異なる必要があります。

このデータは配列に読み込み使います。配列変数は

Public Nx(50),Ny(50),NCD(50)

と宣言します。Nx はx座標，Nyはy座標 NCD は上の式での C_iです。これを実際のデータに読み込むルーチンは次の通りです。

Sub ReadData
   For i=0 to PDEG
     Read Nx(i), Ny(i)
     NCD(i) = Ny(i)
   Next i
End Sub

　NCD(i)= Ny(i) としているのは，後の計算の初期設定のためです。

グラフの初期描画

　グラフィックの設定のため，グラフ画面の左下と右上の座標をそれぞれ，(Xmin,Ymin)，(Xmax,Ymax) として指定することにします。

Xmin = -10 : Xmax = 10
Ymin = -10 : Ymax = 10

　開く画面の大きさはここでは４００×４００の正方形で開きます。背景は紺，座標軸は水色にしました。グラフ画面の初期設定は次の通りです。

Sub GraphInit(Xmin,Xmax,Ymin,YMax)
   BackColor = "Navy"
   GScreen(400,400)
   MathGraph On
   Window (Xmin,Ymin)-(Xmax,Ymax)
   CLS 2
   ForeColor = "Cyan"
   LINE (Xmin,   0)-(Xmax,   0)    : 'x 軸
   LINE (   0,Ymin)-(   0,Ymax)    : 'y 軸
End Sub

　次に入力したデータをグラフ画面に表示します。

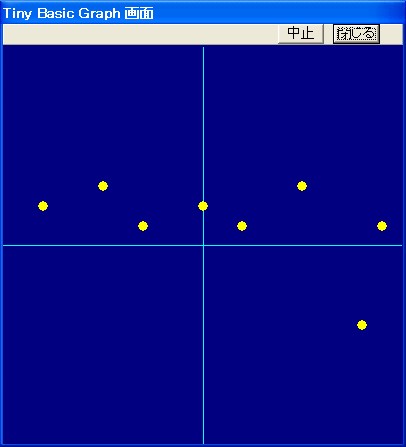
Sub DrawInitData
   ForeColor = "Yellow"
   For i = 0 to PDEG
      Circle (Nx(i),Ny(i)),0.3,,,,,F
   Next i
   ForeColor = "White"
End Sub

入力データを表す点を半径0.3 で黄色ので描きます。

ｆ（ｘ）の計算

　次にニュートン補間して得られる関数f(x) のグラフを描きましょう。

まず，Ci の計算をします。配列NCD(i)を Ciのこととします。上の差分法の結果を使って，順次階差を計算し，それをNCD(i)に入れることにします。

Sub CalcNCD
   For Ni = 1 to PDEG
      For Nj = PDEG to Ni step -1
         NCD(Nj) = (NCD(Nj) - NCD(Nj-1))/(Nx(Nj) - Nx(Nj-Ni))
      Next Nj
   Next Ni
End Sub

　ＮiがNi階の差分を計算する部分です。最終的にNCD(Nj)にはNj階の差分の結果が入るようになります。即ち，上のルーチンを実行すると，C_i=NCD(i) となります。

C_iが計算できたら，f(x) の計算はニュートン補間法の定義式をそのまま使います。

Function Newton(x)
   NewX = NCD(0)
   Prod = 1
   For Ni = 1 to PDEG
      Prod = Prod * (x - Nx(Ni-1))
      NewX = NewX + Prod * NCD(Ni)
   Next Ni
   Newton = NewX
End Function

　これで後は，この関数を使ってグラフを描きます。

Sub DrawGraph(Xmin,Xmax)
   X  = Xmin    
   Y  = Newton(X)
   h  = Xmax -Xmin
   FOR I = 1 TO 80
      X1 = X
      Y1 = Y
      X  = Xmin + h*I/80 
      Y  = Newton(X)
      LINE (X1,Y1)-(X,Y)
   NEXT I
End Sub

実行

　以上の部分に，実行部分を書けばプログラムは完成です。ここでは次の部分を加えました。

完成したプログラムNewtonIP.tbt はここにあります。

   Cls : Print "Newton の補間公式"
   Call  ReadData
   Call  GraphInit(Xmin,Xmax,Ymin,YMax)
   Call  DrawInitData
   Call  CalcNCD
   Input "スタートします。リターンキーを押して下さい。"; Ch
   Call  DrawGraph(Xmin,Xmax)
END

実際に実行すると，まず，入力データが画面に表示されます。

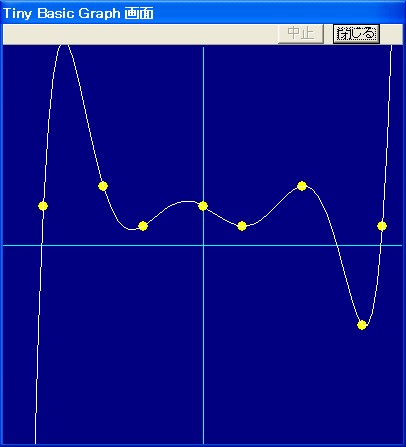
リターンキーを押すと，これらの８個の点を通る７次式で補間され，次の画面になります。

まとめ

　今回作成したプログラムは，ニュートンの補間公式についてのある程度の知識が必要です。プログラムはあくまでも道具ですから，書こうとする対象についての知識は必須です。良いプログラマーはプログラム自身を知るだけでなく，当然ですが，書こうとする対象についても知識が必要です。

プログラム以外に得意な分野を持ちましょう。