| シンプソンの公式 |
シンプソンの公式は数値積分での基本的公式の1つです。ここでは,プログラムのモジュール化の例として,この公式を使って定積分の値を計算するプログラムを作成してみましょう。
シンプソンの公式は高校の数Cの教科書に載っているもので,数値積分での基本的なものです。既に知っている人も多いと思いますが,一通りの復習をして見ましょう。
| シンプソンの公式 |
数値積分は定積分∫f(x)dx (aからbまで)を数値として求める計算法のことです。定積分は不定積分F(x)=∫f(x)dx が求まれば,
∫f(x)dx (aからbまで)=F(b)-F(a)
から求めることができます。この公式(微分積分学の基本定理)は理論としては,これで完璧ですが,実際の値を求めると言う視点からは,まだ十分ではありません。 それは
があるからです。理論的立場からすると,
例を挙げましょう。k2≠1のとき,
また,不定積分が具体的に求められる場合でも,例えば
は良く知られたアークタンジェントについての公式ですが,左辺の積分値と右辺の値を求めるのはどちらが簡単でしょうか。ArcTan(x)の値はx からどのように求めるのでしょうか。
このように,不定積分(原始関数)が求められるかどうかと言うことは別に,積分値を直接計算する方法を求めるのは意義があります。
数値積分は,
f(x) の計算方法が分かっている場合,∫f(x)dx (aからbまで)の値を数値的に求める方法
と言えます。
数値積分は数値計算での基本的問題ですから,色々の方法があります。その中でもシンプソンの公式は,万能ではありませんが,比較的簡単で,精度の良い方法として知られています。
関数f(x) の 区間[a,b]での定積分を求めるとします。[a,b]を2m等分して,a=a0<a1< ・・・ <a2m=b とします。分点 aiでのfの値をそれぞれ,yi とします。即ち yi=f(ai) です。さらに,d=(b-a)/2m とします。このとき,∫f(x)dx (aからbまで)は
|
∫f(x)dx (aからbまで)≒ d(y0+y2m+2(y2+y4+…+y2m-2)+4(y1+y3+…+y2m-1))/3 |
で与えられる。これがシンプソンの公式です。
シンプソンの公式は,関数を放物線で近似して,その値から積分値を求めたものです。精度はd4のオーダー,つまり,dが半分(等分数を2倍)すると,誤差が1/16 になることが示されます。
| プログラムの概要 |
プログラムの概要を考えましょう。シンプソンの公式で計算をするといっても色々なアプローチがあると思いますが,全体の状況が分かるように,次の3つの機能を持つようにします。
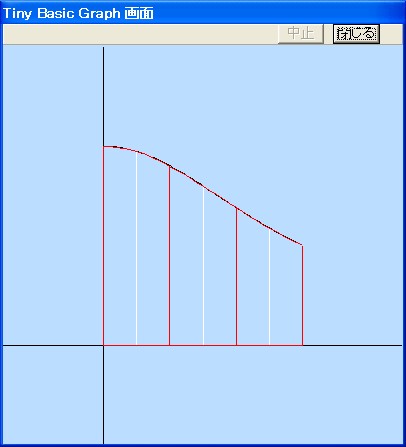
シンプソンの公式の精度はグラフの形に依存します。ですからその状況がグラフからある程度推測できます。滑らかなグラフの場合,少ない等分数でも良い精度が出ます。他方,曲線の傾きが非常に大きい点があると,いくら等分数を増やしても精度はよくなりません。この辺の事情はグラフを見るとかなり分かります。
また,関数f(x) や,積分範囲 [a,b],等分数2mを変更しやすいように配慮します。
さて,以上の処理を実現するプログラムを書いて見ましょう。
| シンプソンの公式による計算値 |
シンプソンの公式をプログラムにするだけですから,簡単です。モジュール化ということで,Function を使うことにします。
以下がそのプログラムです。説明の為,行番号をつけていますが,実際のプログラムにはありません。
01 Function Simpson(a,b,m) 02 d = (b-a)/(2*m) 03 S = F(a) 04 for i=1 to 2*m-1 05 x = a + i * d 06 if (i mod 2)=1 then S= S + 4 * F(x) 07 if (i mod 2)=0 then S= S + 2 * F(x) 08 next i 09 S = S + F(b) 10 Simpson = S * d/3 11 End Function
1行目は名前,Simpson と言う名前をつけました。a,b,mを関数に引き渡します。
2行目はa,b,m からd を求めています。
Sはシンプソンの公式で,y0+y2m+2(y2+y4+…+y2m-2)+4(y1+y3+…+y2m-1)を表します。
y0を加えるのが,3行目です。y2mを加えるのは9行目です。
4行から8行が中間の項の和ですが,奇数番目は4倍して加え,偶数番目は2倍して加えています。
10行目で関数値を決めています。ここで,Simpson(a,b,m)=S*d/3 としてはいけません。
ここで関数f(x)の計算ですが,上のプログラムだけでは出来ません。このf(x)は別に関数として定義します。
01 Function F(x) 02 F = 1/(1+x^2) 03 End Function
としています。このようにすると,2行目の 1/(1+x^2) がF(x)として使えるようになります。Tiny Basic では関数はどこに置いて定義しても,どこからでも使えますから,プログラムの先頭に近い部分に置きます。関数を変える場合はこの2行部分を変更すれば良いだけです。
これだけのプログラムでシンプソンの公式による計算は可能です。例えば
Print Simpson(0,1,3)
とすれば,[0,1]区間で,2*3等分による計算値が得られます。
| f(x)のグラフ |
次に関数f(x) のグラフを描きましょう。この部分は,一般的な平面グラフの描画です。2つの部分に分けて書くことにします。値を返す必要がありませんから,Sub を使うことにします。
まず,グラフ画面の設定。
01 Sub InitGraph(ax,ay,bx,by) 02 BackColor ="#BBDDFF" 03 GScreen(400,400) 04 MathGraph On 05 Window (ax,ay)-(bx,by) 06 ForeColor = "Black" 07 Line (ax,0)-(bx,0) 08 Line (0,ay)-(0,by) 09 End Sub
InitGraph と言う名前の Sub プログラムで,ax,ay,bx,by を引き渡します。ここで(ax,ay)がグラフの左下隅の点,(bx,by) が右上隅の座標です。
2行で,背景色を指定しています。3行でグラフ画面を開きます。大きさ400×400です。ここを変えると大きさが変化します。
4行では座標の向きを下から上への方向に設定します。6行で前景色(グラフを描く色)を指定しています。
6行目はx軸,7行目はy軸を描いています。
次に実際のグラフを各部分です。
01 Sub DrawGraph(a,b) 02 MV=Max(abs(a),abs(b)) 03 ForeColor = "Black" 04 X1 = a : Wd = b-a 05 Y1 = F(X1) 06 For I = 1 TO 100 : '100の点折れ線で描く 07 X2 = a + Wd*I/100 : 'X1の設定 08 Y2 = F(X2) : 'Y1の設定 09 if abs(Y1)<=MV then Line (X1,Y1)-(X2,Y2) 10 X1 = X2 11 Y1 = Y2 12 Next I 13 End Sub
DrawGraph(a,b) は区間[a,b]の範囲でf(x) のグラフを描きます。2行の MV はグラフ画面内を計るためのものですが,グラフによってはもう少し大きくしたほうが良いかもしれません。
3行で前景色の指定,6行から12行で分点を求め,9行でy1の範囲がMV 未満なら,線分を実際に書いています。
| f(x)の近似グラフ |
シンプソンの公式は,区間[a,b]をm 等分した範囲で,その両端と中点でのf(x) の値を求め,それらを通る放物線を考え,その値を計算したものです。放物線は2次式ですから,その不定積分は3次の多項式でその値は簡単に求められます。それを計算し纏めたものがシンプソンの公式です。
そこで,その放物線を繋いで出来るグラフを元々のf(x)のグラフに重ねて見ると,その差が誤差を与えますから,精度について見当がつきます。
この近似グラフを描くのは少し複雑ですから,2つの部分に分けることにします。
2は1を使って描くわけですが,1が出来ればそれほど難しい訳ではありません。1は少し数学的に考える必要があります。
| 2点とその中点でのf(x)の値が与えられたとき,その3点を通る放物線を描く |
問題は次の通りです。
| x0<x1 が与えられたとして,その中点x2を取ります。そしてそこでの値
y0,y1,y2が与えられたとするとき, 3点(x0,y0),(x1,y1),(x2,y2)を通る放物線を描く |
まず,放物線の方程式を求める必要があります。方程式はy=ax^2+bx+c の形をしていますが,この形で考えるよりもグラフの描きやすさから次の形で考えましょう。 0≦t≦1なる変数 t を考え,x=(x1-x0)t+x0とします。放物線を t の関数として,
y=at(t-1)+bt+c
の形で考えます。t=0の時がx0,t=1の時がx1,t=1/2の時が中点x2です。ここで,t=0,1,1/2を上の式に代入して方程式を解くと,
c=y0,b=y1-y0,a=2(y0+y1)-4y2
が得られます。比較的簡単な式ですね。これが得られれば,問題は一般的なプログラミングの問題です。次がそのプログラムです。
01 Sub DrawPCurve(x0,x1) 02 c=F(x0) : b=F(x1)-F(x0) 03 a=2*(F(x0)+F(x1))-4*F((x0+x1)/2) 04 Px0=x0 05 Py0=c 06 For i=1 to 10 07 t=i/10 08 Px1=(x1-x0)*t+x0 09 Py1=a*t*(t-1)+b*t+c 10 Line (Px0,Py0)-(Px1,Py1),12 11 Px0=Px1 12 Py0=Py1 13 Next i 14 End Sub
1行目がSub の名前の指定です。PCurve のPは Parabola(放物線)のつもりです。x0とx1を渡します。
2,3行目は上の計算で得られた,a,b,c を決めています。
放物線のグラフを描くのに,ここでは10本の線分で描きます。各線分の左端が(Px0,Py0),右端が(Px1,Py1)です。
4,5行目で最初の左端を決めています。6から13行目までが,繰り返しですが,tが0から1なので,設定は楽です。
6行目の For文は i=1から10にして,7行目でt=i/10とすると,tが1/10から 1までの範囲を動きます。
8行でxを決め,9行でyを決めます。10行で線分を描き,11行12行では次の線分に移るため,Px0,Py0を再設定しています。
これで1は出来ました。そこで次に2を考えましょう。
| 区間[a,b]での近似グラフを描く。 |
シンプソンの公式の意味したがって,区間[a,b]を2m等分して,各2区間について,放物線を書けば良いわけです。プログラムは次のようになります。
01 Sub DrawSimpson(a,b,m) 02 X1 = a 03 n=2*m 04 d = (b-a)/n 05 Y1 = F(X1) 06 For i = 1 TO 2*m step 2 07 X2 = a + i *d 08 Y2 = F(X2) 09 X3 = a + (i+1) *d 10 Y3 = F(X3) 11 Line (X1,0)-(X1,Y1),12 12 Line (X2,0)-(X2,Y2),15 13 Call DrawPCurve(x1,x3) 14 Line (X3,0)-(X3,Y3),12 15 Line (X3,0)-(X1, 0),12 16 X1 = X3 17 Y1 = Y3 18 Next i 19 End Sub
1行目で Sub の名前を決めます。a,b,mを渡します。2から5行目までが初期設定,nが分割数,dは分割幅です。6行でstep 2とあるのは,各2区間で1つの処理をするためです。
11行,14行,15行で2区間の周りを(近似部分以外を)線で囲みます。12行は中間の縦線です。13行で,近似部分のグラフを描きます。
| 実行例 |
以上で,シンプソンの公式のプログラムのモジュールが全てそろいました。あとはこれを適当に呼べば良いわけです。例えば ,Fやa,b,c,x0,y0,x1,y1,mを適当に設定して
Call InitGraph(x0,y0,x1,y1)
Call DrawGraph(a,b)
Call DrawSimpson(a,b,m)
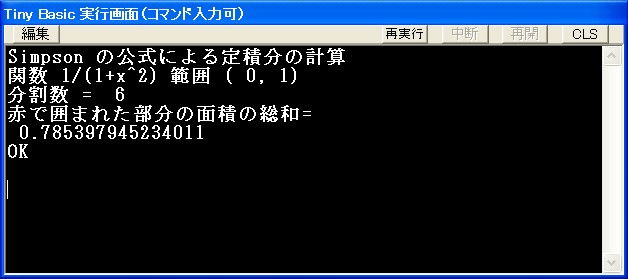
Print "Simpson の公式による定積分の計算"
Print "関数 ";DF$;" 範囲 (";a;",";b;")"
Print "分割数 = ";2*m
Print "赤で囲まれた部分の面積の総和="
Print Simpson(a,b,m)
End
のようにすれば,動作します。 その部分を追加したプログラムSimpson.tbtがここにあります。実行した結果は以下の通りです。

この値はπ/4になりますが,6等分で計算した結果は
4*0.785397945234011=3.14159178093604
です。π=3.14159265358979ですから,小数点以下5桁まで正確です。
| まとめ |
今回作成したプログラムは,Sub と Function がプログラムの大半を占めています。Sub やFunctionは他のプログラムでの流用か比較的容易ですから,このようなプログラムを蓄積していくと,色々なプログラムが比較的短期間に作成出来るでしょう。
プログラムのモジュール化は,プログラムの検証を容易にするだけでなく,再利用も容易にします。!